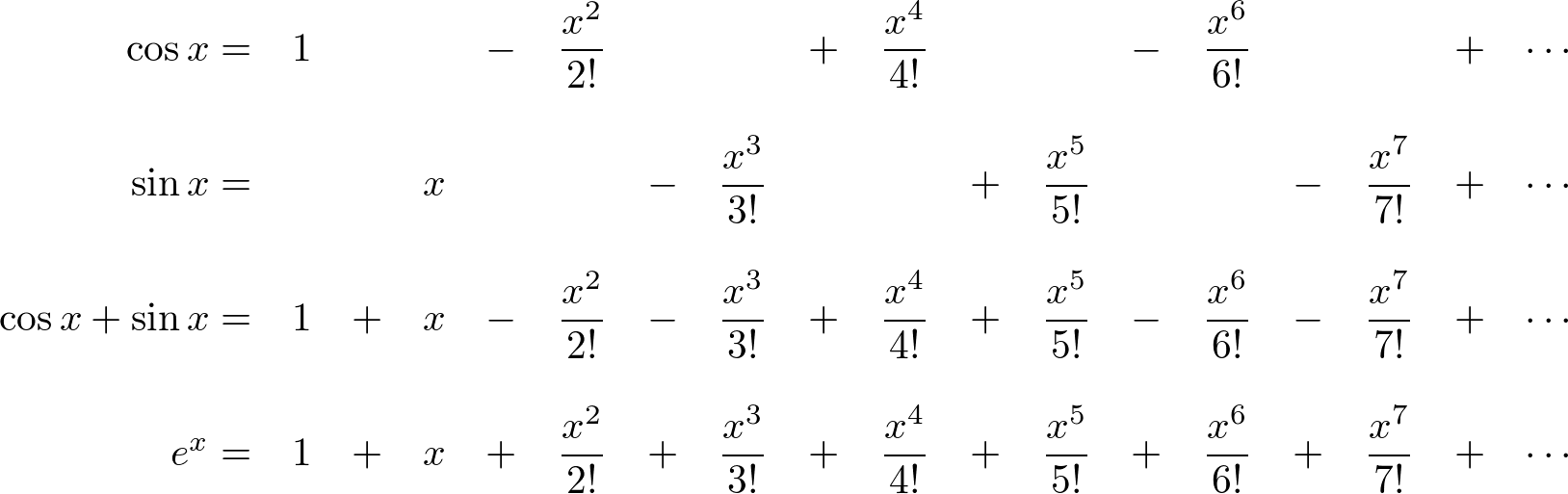Sinx In Exponential Form
Sinx In Exponential Form - This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers. If μ r then eiμ def = cos μ + i sin μ. Periodicity of the imaginary exponential. Expz denotes the exponential function. Web in mathematics, physics and engineering, the sinc function, denoted by sinc (x), has two forms, normalized and unnormalized. The picture of the unit circle and these coordinates looks like this: Web relations between cosine, sine and exponential functions. Sin ( i x) = 1 2 i ( exp ( − x) − exp ( x)) = i sinh ( x). But i could also write the sine function as the imaginary part of the exponential. [1] 0:03 the sinc function as audio, at 2000 hz.
Web notes on the complex exponential and sine functions (x1.5) i. Sin(x) sin ( x) is the fourier series of sin(x) sin ( x) just as eix e i x is the fourier series of eix e i x in exponential form, of course you could write eix = cos(x). E^(ix) = sum_(n=0)^oo (ix)^n/(n!) = sum_(n. Web i know that in general i can use. Sinz denotes the complex sine function. But i could also write the sine function as the imaginary part of the exponential. Periodicity of the imaginary exponential. This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers. For any complex number z : The picture of the unit circle and these coordinates looks like this:
Periodicity of the imaginary exponential. Web i know that in general i can use. E^x = sum_(n=0)^oo x^n/(n!) so: Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. Expz denotes the exponential function. [1] 0:03 the sinc function as audio, at 2000 hz. But i could also write the sine function as the imaginary part of the exponential. Sin(x) sin ( x) is the fourier series of sin(x) sin ( x) just as eix e i x is the fourier series of eix e i x in exponential form, of course you could write eix = cos(x). This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all.
graphs of sinx and cosx in hindi maths YouTube
Sinz denotes the complex sine function. Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. Expz denotes the exponential function. Web notes on the complex exponential and sine functions (x1.5) i. (45) (46) (47) from these relations and the properties.
Proof that the derivative of coshx is sinhx Maths exam, Math videos
If μ r then eiμ def = cos μ + i sin μ. Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. [1] 0:03 the sinc function as audio, at 2000 hz. Web i know that in general i can.
Grade 12 Advanced Functions [licensed for use only
Sin(x) sin ( x) is the fourier series of sin(x) sin ( x) just as eix e i x is the fourier series of eix e i x in exponential form, of course you could write eix = cos(x). Web notes on the complex exponential and sine functions (x1.5) i. Web in mathematics, physics and engineering, the sinc function, denoted.
How to Solve cos(x) + sin(2x) = 0 (Trigonometric Equations) YouTube
Web trigonometric substitution integrals ( inverse functions) derivatives v t e in trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for. But i could also write the sine function as the imaginary part of the exponential. The picture of the unit circle and these coordinates looks like this: Web i know that in general i can.
Solving Exponential Trigonometric Equations 81^sin2x+81^cos^2x=30
If μ r then eiμ def = cos μ + i sin μ. Web trigonometric substitution integrals ( inverse functions) derivatives v t e in trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for. For any complex number z : Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit.
Integral Table Pdf / List Of Integrals Of Exponential Functions Wikipedia
Expz denotes the exponential function. Sin(x) sin ( x) is the fourier series of sin(x) sin ( x) just as eix e i x is the fourier series of eix e i x in exponential form, of course you could write eix = cos(x). But i could also write the sine function as the imaginary part of the exponential. The.
Function For Sine Wave Between Two Exponential Cuves Mathematics
[1] 0:03 the sinc function as audio, at 2000 hz. But i could also write the sine function as the imaginary part of the exponential. This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers. The.
( sinc( F ω ) = /2)
Web i know that in general i can use. Sin ( i x) = 1 2 i ( exp ( − x) − exp ( x)) = i sinh ( x). Periodicity of the imaginary exponential. But i could also write the sine function as the imaginary part of the exponential. Sin(x) sin ( x) is the fourier series of.
Solved 5. Euler's equations are defined as sin (x) cos(x) e"
(45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. Web may 31, 2014 at 18:57. For any complex number z : Sin(x) sin.
How to Integrate Exponential and Trigonometric Functions (e^x)(Sinx
Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. Web may 31, 2014 at 18:57. [1] 0:03 the sinc function as audio, at 2000 hz. Sinz denotes the complex sine function. Web euler’s formula for complex exponentials according to euler,.
E^(Ix) = Sum_(N=0)^Oo (Ix)^N/(N!) = Sum_(N.
Sin(x) sin ( x) is the fourier series of sin(x) sin ( x) just as eix e i x is the fourier series of eix e i x in exponential form, of course you could write eix = cos(x). Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. Expz denotes the exponential function. The picture of the unit circle and these coordinates looks like this:
Web Trigonometric Substitution Integrals ( Inverse Functions) Derivatives V T E In Trigonometry, Trigonometric Identities Are Equalities That Involve Trigonometric Functions And Are True For.
Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. Sinz = exp(iz) − exp( − iz) 2i. This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers. But i could also write the sine function as the imaginary part of the exponential.
Web Notes On The Complex Exponential And Sine Functions (X1.5) I.
Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. [1] 0:03 the sinc function as audio, at 2000 hz. Sinz denotes the complex sine function. Web relations between cosine, sine and exponential functions.
Web In Mathematics, Physics And Engineering, The Sinc Function, Denoted By Sinc (X), Has Two Forms, Normalized And Unnormalized.
Web may 31, 2014 at 18:57. Periodicity of the imaginary exponential. If μ r then eiμ def = cos μ + i sin μ. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all.