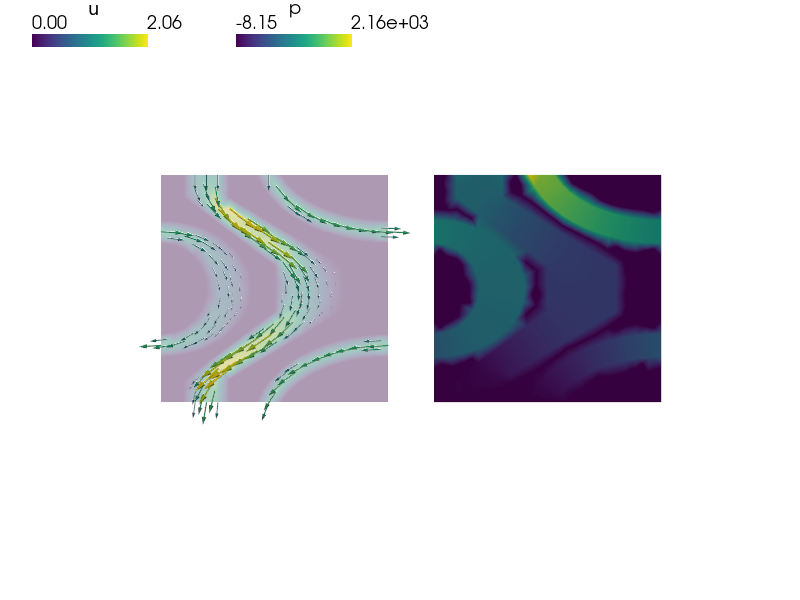
Navier Stokes Vector Form
Navier Stokes Vector Form - If we want to derive the continuity equation in another coordinate system such as the polar, cylindrical or spherical. In the analysis of a flow, it is often desirable to reduce the number of equations and/or the number of variables. Why there are different forms of navier stokes equation? This is enabled by two vector calculus identities: This equation provides a mathematical model of the motion of a. Writing momentum as ρv ρ v gives:. For any differentiable scalar φ and vector a. (10) these form the basis for much of our studies, and it should be noted that the derivation. One can think of ∇ ∙ u as a measure of flow. These may be expressed mathematically as dm dt = 0, (1) and.
If we want to derive the continuity equation in another coordinate system such as the polar, cylindrical or spherical. Web the vector form is more useful than it would first appear. Writing momentum as ρv ρ v gives:. This is enabled by two vector calculus identities: This equation provides a mathematical model of the motion of a. One can think of ∇ ∙ u as a measure of flow. Web 1 answer sorted by: These may be expressed mathematically as dm dt = 0, (1) and. Web where biis the vector of body forces. For any differentiable scalar φ and vector a.
For any differentiable scalar φ and vector a. Web the vector form is more useful than it would first appear. This is enabled by two vector calculus identities: These may be expressed mathematically as dm dt = 0, (1) and. This equation provides a mathematical model of the motion of a. Web where biis the vector of body forces. Why there are different forms of navier stokes equation? One can think of ∇ ∙ u as a measure of flow. If we want to derive the continuity equation in another coordinate system such as the polar, cylindrical or spherical. (10) these form the basis for much of our studies, and it should be noted that the derivation.
(PDF) Closed form solutions for the SteadyState
One can think of ∇ ∙ u as a measure of flow. Web where biis the vector of body forces. For any differentiable scalar φ and vector a. Web the vector form is more useful than it would first appear. (10) these form the basis for much of our studies, and it should be noted that the derivation.
Solved Start from the NavierStokes equation in vector form.
In the analysis of a flow, it is often desirable to reduce the number of equations and/or the number of variables. These may be expressed mathematically as dm dt = 0, (1) and. (10) these form the basis for much of our studies, and it should be noted that the derivation. Writing momentum as ρv ρ v gives:. This is.
The many forms of NavierStokes YouTube
(10) these form the basis for much of our studies, and it should be noted that the derivation. This is enabled by two vector calculus identities: In the analysis of a flow, it is often desirable to reduce the number of equations and/or the number of variables. One can think of ∇ ∙ u as a measure of flow. Web.
PPT Chapter 9 Differential Analysis of Fluid Flow PowerPoint
Web where biis the vector of body forces. (10) these form the basis for much of our studies, and it should be noted that the derivation. This equation provides a mathematical model of the motion of a. In the analysis of a flow, it is often desirable to reduce the number of equations and/or the number of variables. If we.
Resources ME 517 Lecture 19 Microfluidics Continuum
For any differentiable scalar φ and vector a. In the analysis of a flow, it is often desirable to reduce the number of equations and/or the number of variables. These may be expressed mathematically as dm dt = 0, (1) and. One can think of ∇ ∙ u as a measure of flow. This equation provides a mathematical model of.
NavierStokes Equations Equations, Physics and mathematics
If we want to derive the continuity equation in another coordinate system such as the polar, cylindrical or spherical. Web the vector form is more useful than it would first appear. Web 1 answer sorted by: Writing momentum as ρv ρ v gives:. Web where biis the vector of body forces.
navier_stokes/stokes.py — SfePy version 2021.2 documentation
(10) these form the basis for much of our studies, and it should be noted that the derivation. Web 1 answer sorted by: In the analysis of a flow, it is often desirable to reduce the number of equations and/or the number of variables. If we want to derive the continuity equation in another coordinate system such as the polar,.
The NavierStokes equations of fluid dynamics in threedimensional
One can think of ∇ ∙ u as a measure of flow. These may be expressed mathematically as dm dt = 0, (1) and. Writing momentum as ρv ρ v gives:. This is enabled by two vector calculus identities: For any differentiable scalar φ and vector a.
PPT Chapter 9 Differential Analysis of Fluid Flow PowerPoint
These may be expressed mathematically as dm dt = 0, (1) and. If we want to derive the continuity equation in another coordinate system such as the polar, cylindrical or spherical. (10) these form the basis for much of our studies, and it should be noted that the derivation. Web where biis the vector of body forces. Why there are.
NavierStokes Equations Definition & Solution
For any differentiable scalar φ and vector a. If we want to derive the continuity equation in another coordinate system such as the polar, cylindrical or spherical. These may be expressed mathematically as dm dt = 0, (1) and. (10) these form the basis for much of our studies, and it should be noted that the derivation. Web the vector.
This Is Enabled By Two Vector Calculus Identities:
These may be expressed mathematically as dm dt = 0, (1) and. Why there are different forms of navier stokes equation? One can think of ∇ ∙ u as a measure of flow. If we want to derive the continuity equation in another coordinate system such as the polar, cylindrical or spherical.
Writing Momentum As Ρv Ρ V Gives:.
For any differentiable scalar φ and vector a. (10) these form the basis for much of our studies, and it should be noted that the derivation. This equation provides a mathematical model of the motion of a. In the analysis of a flow, it is often desirable to reduce the number of equations and/or the number of variables.
Web The Vector Form Is More Useful Than It Would First Appear.
Web where biis the vector of body forces. Web 1 answer sorted by: