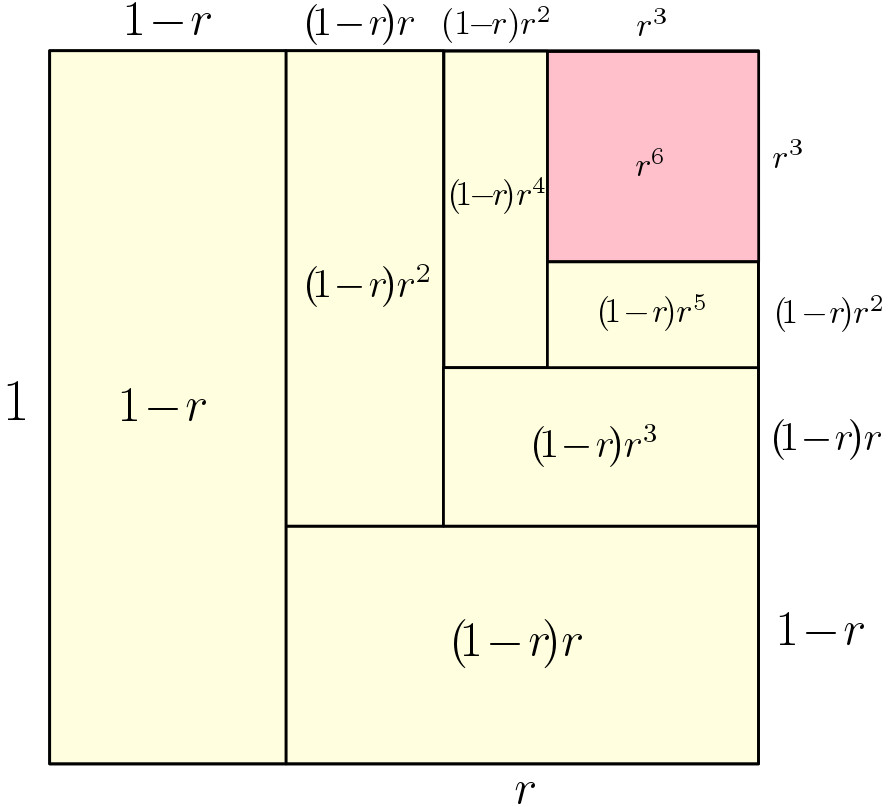
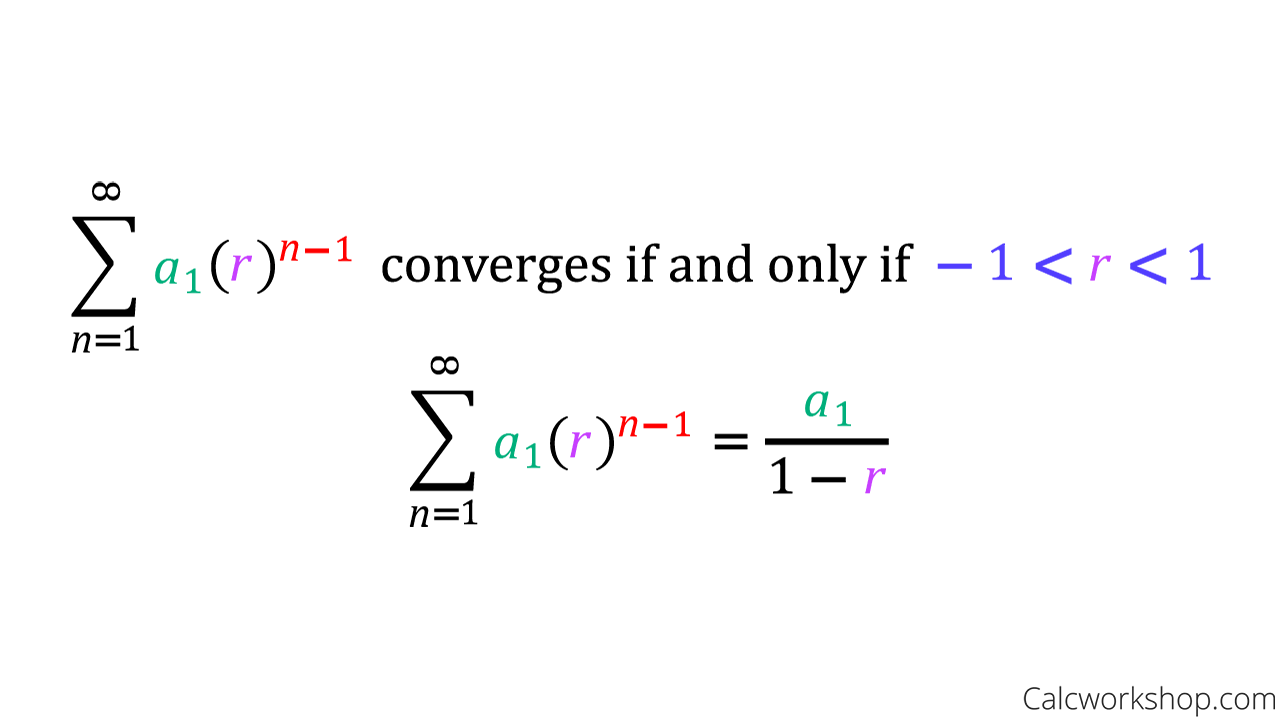Geometric Series Closed Form
Geometric Series Closed Form - Web i theorem:closed form of geometric series ( r 6= 1 ): Suppose the initial term \(a_0\) is \(a\) and the common ratio is \(r\text{.}\). Xxxx3 = x2 ⋅ r = 3 ⋅ ( 5 4)2. Xxxx2 = 3 ⋅ (5 4)1. Web this is the same geometric series, except missing the first two terms. I let's prove why this closed form is correct is l dillig,. $$g(n) = 1 + c^2 + c^3 +. If you look at other textbooks or online, you might find that their closed formulas for arithmetic and geometric sequences. Xxxx4 = x3 ⋅ r = 3 ⋅ ( 5 4)3. Xn j=0 (ar j) = a rn +1 i1 r 1 i this is very useful to know{ memorize it!
Web geometric series consider \(\displaystyle \sum_{n=0}^{\infty} \frac{2}{5^n}\). Xxxx2 = 3 ⋅ (5 4)1. Web xxxr = 15 2 3 = 75 4 15 2 = 375 8 75 4 = 5 2. Once you have that, you should prove by induction that it actually does satisfy your original recurrence. And with r = 5 2. 2 if you remember how the proof of the convergence and sum for a real geometric series goes, that proof works directly for the complex case too. How does one determine if the following series is arithmetic or geometric? These two examples clearly show how we can apply the two formulas to simplify the sum of infinite and finite geometric series. Web find the closed form solution to a geometric series not starting at 0. Web 1 answer sorted by:
An is the nth term of the sequence. Web to write the explicit or closed form of a geometric sequence, we use. These two examples clearly show how we can apply the two formulas to simplify the sum of infinite and finite geometric series. Web this is the same geometric series, except missing the first two terms. A sequence is called geometric if the ratio between successive terms is constant. N f (n) σ 0 1 1 1 5 6 2 14 20 3 30 50 4. Once you have that, you should prove by induction that it actually does satisfy your original recurrence. Xn j=0 (ar j) = a rn +1 i1 r 1 i this is very useful to know{ memorize it! Web to find a closed formula, first write out the sequence in general: If you look at other textbooks or online, you might find that their closed formulas for arithmetic and geometric sequences.
Tutorial Geometric series closedform equation YouTube
Web a geometric sequence18, or geometric progression19, is a sequence of numbers where each successive number is the product of the previous number and. A0 = a a1 = a0 + d = a + d a2 = a1 + d = a + d + d = a + 2d a3 = a2 + d = a + 2d.
PPT Chapter 4 Sequences and Mathematical Induction PowerPoint
N f (n) σ 0 1 1 1 5 6 2 14 20 3 30 50 4. A0 = a a1 = a0 + d = a + d a2 = a1 + d = a + d + d = a + 2d a3 = a2 + d = a + 2d + d = a + 3d ⋮.
calculus A closed form for the sum of (e(1+1/n)^n) over n
An is the nth term of the sequence. Web we discuss how to develop hypotheses and conditions for a theorem; Web geometric series consider \(\displaystyle \sum_{n=0}^{\infty} \frac{2}{5^n}\). Xxxx2 = 3 ⋅ (5 4)1. If you look at other textbooks or online, you might find that their closed formulas for arithmetic and geometric sequences.
Geometric Series YouTube
These two examples clearly show how we can apply the two formulas to simplify the sum of infinite and finite geometric series. Culminating in the closed form of the geometric series, along with a few quick examples. Xxxx4 = x3 ⋅ r = 3 ⋅ ( 5 4)3. N f (n) σ 0 1 1 1 5 6 2 14.
The sum of a geometric series is all you need! Machine Learning
And with r = 5 2. Web this is the same geometric series, except missing the first two terms. Culminating in the closed form of the geometric series, along with a few quick examples. Xn j=0 (ar j) = a rn +1 i1 r 1 i this is very useful to know{ memorize it! Web find the closed form solution.
Find a closedform for the geometric series and d…
Web a geometric sequence18, or geometric progression19, is a sequence of numbers where each successive number is the product of the previous number and. Web this is the same geometric series, except missing the first two terms. $$g(n) = 1 + c^2 + c^3 +. I let's prove why this closed form is correct is l dillig,. Xxxx4 = x3.
What Is The Formula For Geometric Sequence slideshare
If you look at other textbooks or online, you might find that their closed formulas for arithmetic and geometric sequences. N f (n) σ 0 1 1 1 5 6 2 14 20 3 30 50 4. Web i have the following equation: Web geometric series consider \(\displaystyle \sum_{n=0}^{\infty} \frac{2}{5^n}\). When writing the general expression for a geometric sequence, you.
Geometric Series YouTube
Web i have the following equation: 2 if you remember how the proof of the convergence and sum for a real geometric series goes, that proof works directly for the complex case too. I know it's a geometric. Web which is just a geometric series, for which you should know a closed form. A sequence is called geometric if the.
What Is The Formula For Geometric Sequence slideshare
Web this is the same geometric series, except missing the first two terms. The interval of convergence is , since this is when the inside of the general term is and. Web to write the explicit or closed form of a geometric sequence, we use. Web which is just a geometric series, for which you should know a closed form..
Finding a closed form from a recursively defined sequence YouTube
These two examples clearly show how we can apply the two formulas to simplify the sum of infinite and finite geometric series. Web we discuss how to develop hypotheses and conditions for a theorem; Xn j=0 (ar j) = a rn +1 i1 r 1 i this is very useful to know{ memorize it! The most basic tool used to.
Web How To Find The Closed Form Definition Of A Series?
And with r = 5 2. Web this is the same geometric series, except missing the first two terms. The most basic tool used to express generating functions in closed form is the closed form expression for. Web which is just a geometric series, for which you should know a closed form.
Web I Have The Following Equation:
Web closed form expressions for generating functions. When writing the general expression for a geometric sequence, you will. Xxxx2 = 3 ⋅ (5 4)1. Web we discuss how to develop hypotheses and conditions for a theorem;
Web Xxxr = 15 2 3 = 75 4 15 2 = 375 8 75 4 = 5 2.
Web 1 answer sorted by: 2 if you remember how the proof of the convergence and sum for a real geometric series goes, that proof works directly for the complex case too. Xxxx3 = x2 ⋅ r = 3 ⋅ ( 5 4)2. These two examples clearly show how we can apply the two formulas to simplify the sum of infinite and finite geometric series.
A Sequence Is Called Geometric If The Ratio Between Successive Terms Is Constant.
How does one determine if the following series is arithmetic or geometric? Once you have that, you should prove by induction that it actually does satisfy your original recurrence. Culminating in the closed form of the geometric series, along with a few quick examples. A0 = a a1 = a0 + d = a + d a2 = a1 + d = a + d + d = a + 2d a3 = a2 + d = a + 2d + d = a + 3d ⋮ we see that to find.