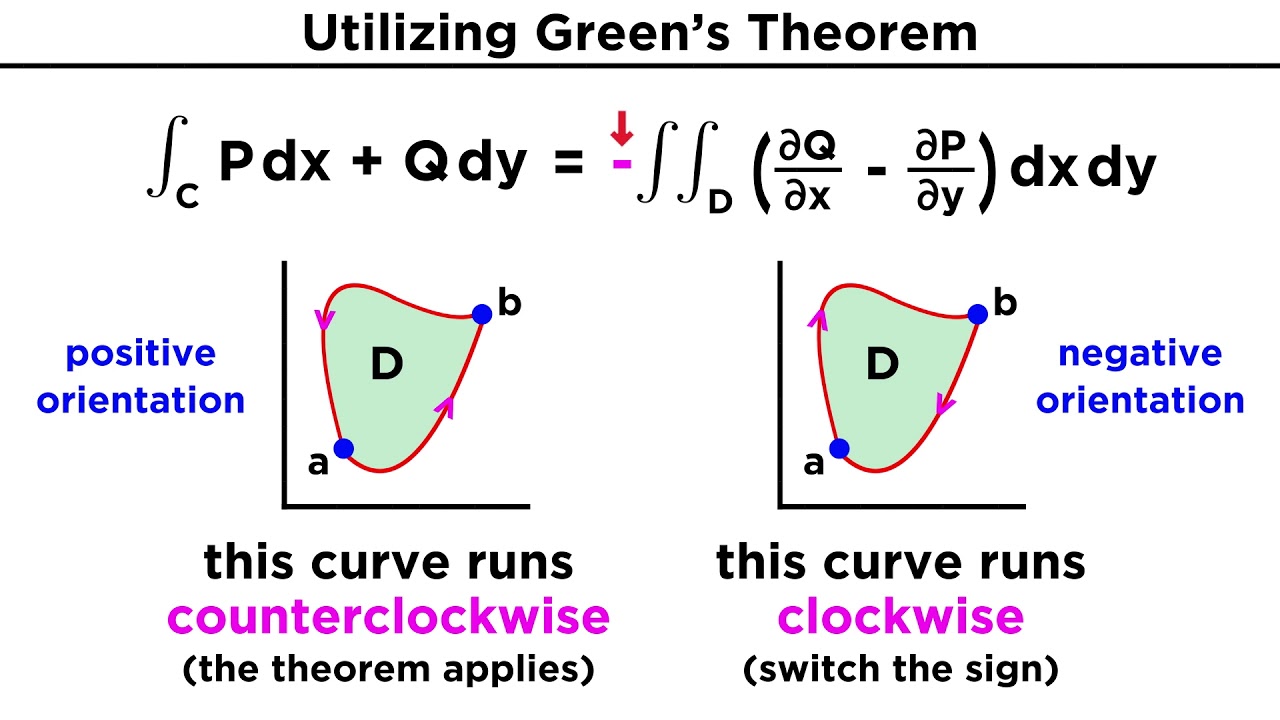
Green's Theorem Flux Form
Green's Theorem Flux Form - Green’s theorem has two forms: Web multivariable calculus unit 5: Heat flux reduction depends on the building and roof insulation and moisture in a green roof’s soil medium. Web math article green’s theorem green’s theorem green’s theorem is mainly used for the integration of the line combined with a curved plane. The line integral in question is the work done by the vector field. Web in vector calculus, green's theorem relates a line integral around a simple closed curve c to a double integral over the plane region d bounded by c. Web green's theorem is a vector identity which is equivalent to the curl theorem in the plane. Web mail completed form to: Web key equations green’s theorem, circulation form ∮cp dx+qdy= ∬dqx −p yda ∮ c p d x + q d y = ∬ d q x − p y d a, where c c is the boundary of d d green’s theorem, flux. Web the two forms of green’s theorem green’s theorem is another higher dimensional analogue of the fundamentaltheorem of calculus:
Web reduced pressure principle assembly double check valve assembly air gap required separation initial test date _____ time_____ leaked closed tight held at_____psid Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form, emphasizing that the theorem is a shortcut for line. Web green’s theorem in normal form 1. Web the two forms of green’s theorem green’s theorem is another higher dimensional analogue of the fundamentaltheorem of calculus: Web in vector calculus, green's theorem relates a line integral around a simple closed curve c to a double integral over the plane region d bounded by c. In this section, we examine green’s theorem, which is an extension of the fundamental theorem of calculus to two dimensions. Web it is my understanding that green's theorem for flux and divergence says ∫ c φf =∫ c pdy − qdx =∬ r ∇ ⋅f da ∫ c φ f → = ∫ c p d y − q d x = ∬ r ∇ ⋅ f → d a if f =[p q] f → = [. Over a region in the plane with boundary , green's theorem states (1). It relates the line integral of a vector. Green's, stokes', and the divergence theorems 600 possible mastery points about this unit here we cover four different ways to extend the.
Web multivariable calculus unit 5: Web in this section, we examine green’s theorem, which is an extension of the fundamental theorem of calculus to two dimensions. Web in vector calculus, green's theorem relates a line integral around a simple closed curve c to a double integral over the plane region d bounded by c. Typically, it can lower the need for air conditioning load to cool. Heat flux reduction depends on the building and roof insulation and moisture in a green roof’s soil medium. Web reduced pressure principle assembly double check valve assembly air gap required separation initial test date _____ time_____ leaked closed tight held at_____psid Web mail completed form to: The flux of a fluid across a curve can be difficult to calculate using. Over a region in the plane with boundary , green's theorem states (1). The line integral in question is the work done by the vector field.
Green's Theorem YouTube
The double integral uses the curl of the vector field. Web multivariable calculus unit 5: Web first we will give green’s theorem in work form. The flux of a fluid across a curve can be difficult to calculate using. Heat flux reduction depends on the building and roof insulation and moisture in a green roof’s soil medium.
Daily Chaos Green's Theorem and its Application
The double integral uses the curl of the vector field. Web multivariable calculus unit 5: The flux of a fluid across a curve can be difficult to calculate using. Web key equations green’s theorem, circulation form ∮cp dx+qdy= ∬dqx −p yda ∮ c p d x + q d y = ∬ d q x − p y d a,.
Determine the Flux of a 2D Vector Field Using Green's Theorem (Hole
Green’s theorem has two forms: Web key equations green’s theorem, circulation form ∮cp dx+qdy= ∬dqx −p yda ∮ c p d x + q d y = ∬ d q x − p y d a, where c c is the boundary of d d green’s theorem, flux. Web green’s theorem in normal form 1. Web green's theorem is a.
multivariable calculus How are the two forms of Green's theorem are
Green's theorem proof (part 1) green's theorem proof (part 2) green's theorem example 1. The line integral in question is the work done by the vector field. Web in this section, we examine green’s theorem, which is an extension of the fundamental theorem of calculus to two dimensions. Web first we will give green’s theorem in work form. Web the.
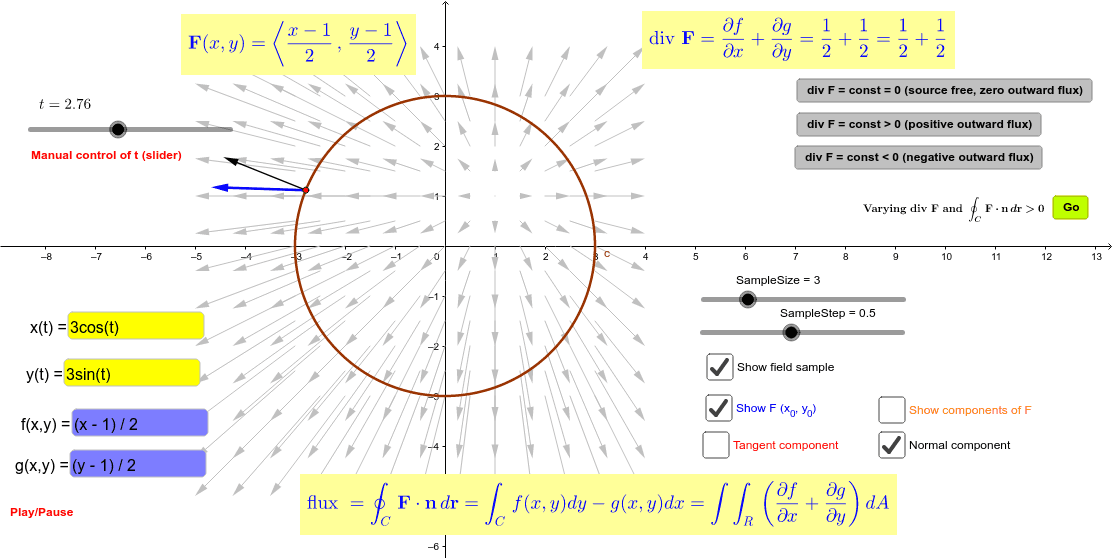
Illustration of the flux form of the Green's Theorem GeoGebra
Green's, stokes', and the divergence theorems 600 possible mastery points about this unit here we cover four different ways to extend the. Web multivariable calculus unit 5: Web key equations green’s theorem, circulation form ∮cp dx+qdy= ∬dqx −p yda ∮ c p d x + q d y = ∬ d q x − p y d a, where c.
Determine the Flux of a 2D Vector Field Using Green's Theorem (Parabola
Green’s theorem has two forms: Web the flux form of green’s theorem relates a double integral over region d d to the flux across boundary c c. Web math article green’s theorem green’s theorem green’s theorem is mainly used for the integration of the line combined with a curved plane. Web the two forms of green’s theorem green’s theorem is.
Green's Theorem Example 1 YouTube
Green’s theorem has two forms: The double integral uses the curl of the vector field. Heat flux reduction depends on the building and roof insulation and moisture in a green roof’s soil medium. Web key equations green’s theorem, circulation form ∮cp dx+qdy= ∬dqx −p yda ∮ c p d x + q d y = ∬ d q x −.
Green's Theorem Flux Form YouTube
Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form, emphasizing that the theorem is a shortcut for line. Web in vector calculus, green's theorem relates a line integral around a simple closed curve c to a double integral over the plane region d bounded by c. The double integral.
Flux Form of Green's Theorem YouTube
Web it is my understanding that green's theorem for flux and divergence says ∫ c φf =∫ c pdy − qdx =∬ r ∇ ⋅f da ∫ c φ f → = ∫ c p d y − q d x = ∬ r ∇ ⋅ f → d a if f =[p q] f → = [. Web the.
Determine the Flux of a 2D Vector Field Using Green's Theorem
Over a region in the plane with boundary , green's theorem states (1). Web green's theorem in normal form green's theorem for flux. Web in the circuit court of clay county, missouri seventh judicial circuit of missouri liberty, missouri precept for witnesses state of missouri case number_____ Green's theorem proof (part 1) green's theorem proof (part 2) green's theorem example.
Web Reduced Pressure Principle Assembly Double Check Valve Assembly Air Gap Required Separation Initial Test Date _____ Time_____ Leaked Closed Tight Held At_____Psid
Web green's theorem is a vector identity which is equivalent to the curl theorem in the plane. In this section, we examine green’s theorem, which is an extension of the fundamental theorem of calculus to two dimensions. The line integral in question is the work done by the vector field. Web in the circuit court of clay county, missouri seventh judicial circuit of missouri liberty, missouri precept for witnesses state of missouri case number_____
Web In This Section, We Examine Green’s Theorem, Which Is An Extension Of The Fundamental Theorem Of Calculus To Two Dimensions.
Web multivariable calculus unit 5: Web the two forms of green’s theorem green’s theorem is another higher dimensional analogue of the fundamentaltheorem of calculus: Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form, emphasizing that the theorem is a shortcut for line. Web in vector calculus, green's theorem relates a line integral around a simple closed curve c to a double integral over the plane region d bounded by c.
Typically, It Can Lower The Need For Air Conditioning Load To Cool.
Web math article green’s theorem green’s theorem green’s theorem is mainly used for the integration of the line combined with a curved plane. Web green’s theorem in normal form 1. Web first we will give green’s theorem in work form. Web it is my understanding that green's theorem for flux and divergence says ∫ c φf =∫ c pdy − qdx =∬ r ∇ ⋅f da ∫ c φ f → = ∫ c p d y − q d x = ∬ r ∇ ⋅ f → d a if f =[p q] f → = [.
Green’s Theorem Has Two Forms:
The flux of a fluid across a curve can be difficult to calculate using. It relates the line integral of a vector. Heat flux reduction depends on the building and roof insulation and moisture in a green roof’s soil medium. Green's theorem proof (part 1) green's theorem proof (part 2) green's theorem example 1.